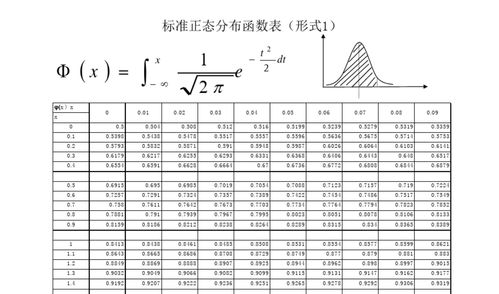
标准正态分布概述。

标准正态分布，又称为标准正态分布（StandardNormalDistribution），是一种特殊的正态分布，其均值为0，标准差为1。在统计学和概率论中，标准正态分布是一个非常重要的概念，因为它为数据标准化提供了一个基础，使得不同分布的数据可以进行比较和分析。。

。

。

标准正态分布的定义与特性。

标准正态分布的概率密度函数（PDF）可以表示为：。

。

\\[f(x)=\\frac{1}{\\sqrt{2\\pi}}e^{-\\frac{x^2}{2}}\\]。

其中，\\(x\\)是随机变量，\\(\\sqrt{2\\pi}\\)是常数，\\(e\\)是自然对数的底数。。

。

标准正态分布具有以下特性：。

。

。

对称性：标准正态分布是以0为中心对称的。。

均值与标准差：均值为0，标准差为1。。

68-95-99.7规则：在标准正态分布中，约68的数据点位于均值加减1个标准差的范围内，约95的数据点位于均值加减2个标准差的范围内，约99.7的数据点位于均值加减3个标准差的范围内。。

。

。

标准正态分布的应用。

标准正态分布在多个领域都有广泛的应用，以下是一些常见的应用场景：。

。

。

统计学：在假设检验、置信区间估计、回归分析等统计方法中，标准正态分布是重要的参考分布。。

工程学：在质量控制、可靠性分析、信号处理等领域，标准正态分布用于评估系统的性能和可靠性。。

医学：在生物统计学、流行病学、临床试验等领域，标准正态分布用于分析数据、评估治疗效果和预测疾病风险。。

金融学：在风险管理、资产定价、投资组合优化等领域，标准正态分布用于评估金融市场的风险和收益。。

。

。

标准正态分布的绘图。

在Python中，可以使用matplotlib库绘制标准正态分布的概率密度曲线（PDF）和累积概率密度函数（CDF）。。

。

```python。

importnumpyasnp。

importmatplotlib.pyplotasplt。

。

生成标准正态分布的数据。

x=np.linspace(-4,4,1000)。

pdf=(1/np.sqrt(2np.pi))np.exp(-x2/2)。

cdf=np.cumsum(pdf)。

。

绘制PDF曲线。

plt.figure(figsize=(10,6))。

plt.plot(x,pdf,label='PDF')。

plt.title('标准正态分布的概率密度曲线')。

plt.xlabel('x')。

plt.ylabel('概率密度')。

plt.legend()。

plt.grid(True)。

plt.show()。

。

绘制CDF曲线。

plt.figure(figsize=(10,6))。

plt.plot(x,cdf,label='CDF')。

plt.title('标准正态分布的累积概率密度函数')。

plt.xlabel('x')。

plt.ylabel('累积概率密度')。

plt.legend()。

plt.grid(True)。

plt.show()。

```。

。

标准正态分布的Z分数。

标准正态分布的Z分数，也称为标准分数，是一种将任意分布的数据转换为标准正态分布的统计量。Z分数的计算公式如下：。

。

\\[Z=\\frac{X-\\mu}{\\sigma}\\]。

其中，\\(X\\)是原始数据，\\(\\mu\\)是原始数据的均值，\\(\\sigma\\)是原始数据的标准差。。

。

通过计算Z分数，可以将不同分布的数据进行比较和分析，从而更好地理解数据的分布特征。。

。

。

标准正态分布是一种特殊的正态分布，在统计学和概率论中具有广泛的应用。通过本文的介绍，读者可以了解到标准正态分布的定义、特性、应用以及绘图方法。在实际应用中，标准正态分布可以帮助我们更好地理解和分析数据，为各种领域的研究提供有力支持。。

。